Foundations: Algebra
About this unit
This unit introduces you to the foundational Algebra skills you’ll need for the SAT Math test, starting with more basic examples. Work through the skills one by one or take a unit test to test all of them at once. Learn more about planning your SAT prep in Unit 1: About the digital SAT.
Solving linear equations and inequalities: foundations
What are linear equations and inequalities?
Linear equations and inequalities are composed of constants and variables.
Linear equations use the equal sign (=).
Linear inequalities use inequality signs ( >, < ).
- Solve linear equations
- Solve linear inequalities
- Recognize the conditions under which a linear equation has one solution, no solution, and infinitely many solutions
2x+1-1 = 5 -1 ( Subtract 1 from both the sides )
Linear equation word problems: foundations
What are linear relationships?
A linear relationship is any relationship between two variables that creates a line when graphed in the xy-plane. Linear relationships are very common in everyday life.
In this lesson, we’ll:
- Review the basics of linear relationships
- Practice writing linear equations based on word problems
- Identify the important features of linear functions
The skills covered here will be important for the following SAT lessons:
- Graphs of linear equations and functions
- Systems of linear equations word problems
- Linear inequality word problems
- Graphs of linear systems and inequalities
You can learn anything. Let’s do this!!
(Ans): We’re given three important values here: 17000,5000 and 240.
$17000 is the total price, so that’s what everything else needs to add up to.
$5000 is a one-time payment.
$240 is a constant amount that’s paid every month, so it needs to be multiplied by m,the number of months.
The total price $17000, equals the sum of the other payments: the initial $5000 payment and the $240 paid each month (m).
17000=5000 + 240m.
Linear relationship word problems: foundations
What are linear relationships?
A linear relationship is any relationship between two variables that creates a line when graphed in the xy-plane. Linear relationships are very common in everyday life.
In this lesson, we’ll:
- Review the basics of linear relationships
- Practice writing linear equations based on word problems
- Identify the important features of linear functions
The skills covered here will be important for the following SAT lessons:
- Graphs of linear equations and functions
- Systems of linear equations word problems
- Linear inequality word problems
- Graphs of linear systems and inequalities
You can learn anything. Let’s do this!!
(Ans): We’re given three important values here: 17000,5000 and 240.
$17000 is the total price, so that’s what everything else needs to add up to.
$5000 is a one-time payment.
$240 is a constant amount that’s paid every month, so it needs to be multiplied by m,the number of months.
The total price $17000, equals the sum of the other payments: the initial $5000 payment and the $240 paid each month (m).
17000=5000 + 240m.
Graphs of linear equations and functions: foundations
What are graphs of linear equations and functions questions?
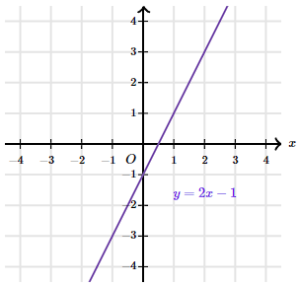
- Identify features of linear graphs from their equations
- Write linear equations based on graphical features
- Determine the equations of parallel and perpendicular lines
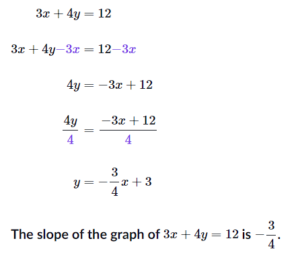
Solving systems of linear equations: foundations
What are systems of linear equations?
- x + y = 5 and 2x – y = 1 are both linear equations with two variables.
- When considered together, they form a system of linear equations.
- (2,3) is the only solution to both x + y = 5 and 2x – y = 1 .
- Look at two ways to solve systems of linear equations algebraically: substitution and elimination.
- Look at systems of linear equations graphically to help us understand when systems of linear equations have one solution, no solutions, or infinitely many solutions.
- Explore algebraic methods of identifying the number of solutions that exist for systems with two linear equations.

